Hello people…! In this post I will explain one of the most widely used Graph Search Algorithms, the Breadth First Search (BFS) Algorithm. Once you have learned this, you would have gained a new weapon in your arsenal, and you can start solving good number of Graph Theory related competitive programming questions.
What we do in a BFS is a simple step-by-step process, which is –
- Start from a vertex S. Let this vertex be at, what is called…. “Level 0”.
- Find all the other vertices that are immediately accessible from this starting vertex S, i.e., they are only a single edge away (the adjacent vertices).
- Mark these adjacent vertices to be at “Level 1”.
- There will be a challenge that you might be coming back to the same vertex due to a loop or a ring in the graph. If this happens your BFS will take ∞ time. So, you will go only to those vertices who do not have their “Level” set to some value.
- Mark which is the parent vertex of the current vertex you’re at, i.e., the vertex from which you accessed the current vertex. Do this for all the vertices at Level 1.
- Now, find all those vertices that are a single edge away from all the vertices which are at “Level 1”. These new set of vertices will be at “Level 2”.
- Repeat this process until you run out of graph.
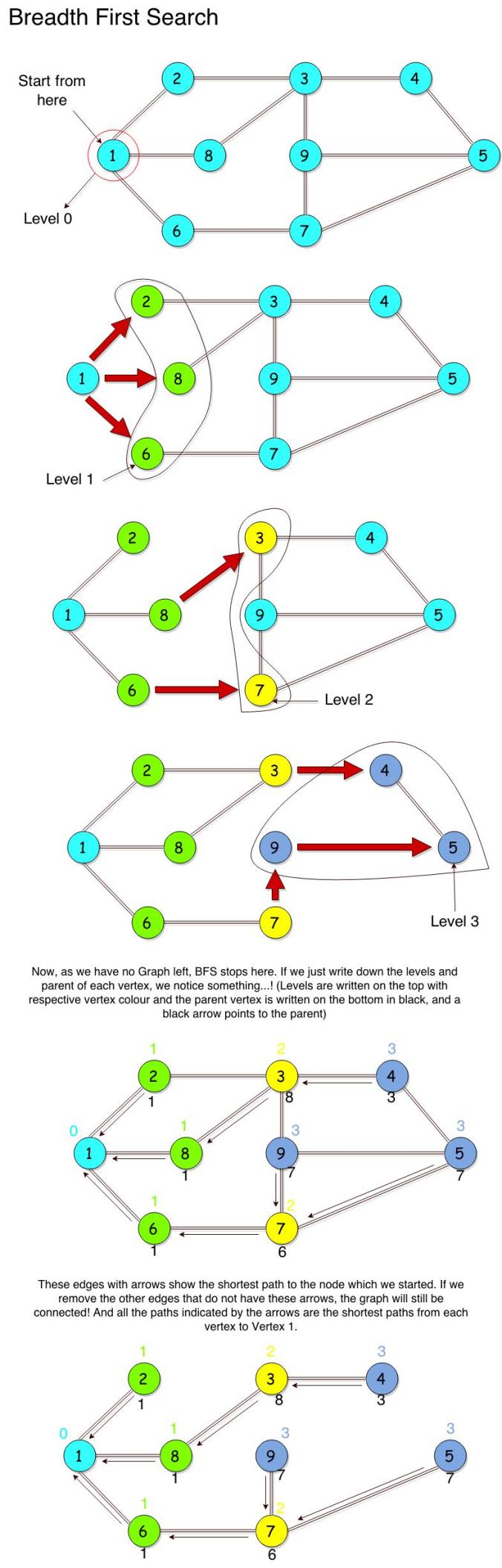
This might sound heavy… Well atleast it would sound heavy to me if I heard it for the first time…! Many questions may pop-up in your mind, like, “How are we gonna do all that…?!”. Well, for now, focus on the concept, we will talk about the code later. And remember, we are talking about an Undirected Graph here. We will talk about Directed Graphs later. To understand the above stated steps, examine the picture below –
The sketch clearly shows you how we explore the vertices adjacent to a vertex and mark their levels. If you have noticed, whenever there were two ways of accessing the same vertex from multiple vertices of the same Level, i.e., in the diagram, Vertex 3 was accessible from Vertex 2 and Vertex 8, we preferred its parent to be Vertex 8, the larger number. Why is that so…? We will learn that in a short moment.
The concepts that I wish to emphasize from the above picture are, how BFS can tell you the shortest path from a given vertex (the start vertex) to all the other vertices and the number of edges or, the “length of the path”, would be the Level of that Vertex itself. This is a very important feature of the BFS, you will understand this more clearly when I explain it with the help of an example in a different post.
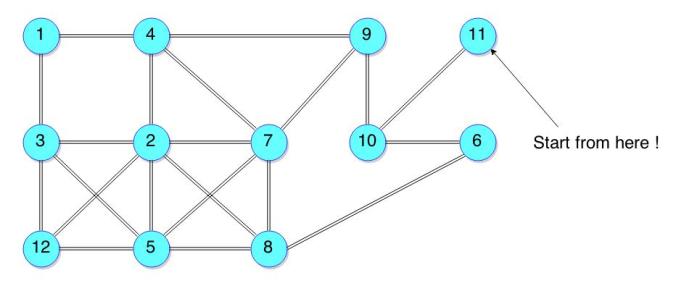
Now, having got some knowledge about the BFS, it is a good thing to do an exercise on this topic to really get the flow going. Try applying BFS on the Graph given. All you have to do is to implement the step-by-step process and get that final figure which I got above. And make sure you label the Levels and Parents for each vertex in the end.
Now, we come to the code part of the Breadth First Search, in C. We use the same Adjacency List that we used in our discussion of Graph Theory Basics. Coming back to our BFS discussion, the level of each vertex is stored in a separate array and so is the case for parent of each vertex. The three arrays are initialized to appropriate values. Now recall our step-by-step process that was stated earlier. Try to put that in terms of pseudocode and then proper code. Take a while to think how you would do that. If you could code it, you are marvelous…! 😀 … If not, don’t fret, I put my code below…!
/* ========== ========== ========== ========= */
// Breadth First Search (BFS) //
// Algorithm in C //
// //
// Functions follow Pascal Case //
// Convention and Variables //
// follow Camel Case Convention //
// //
// Author - Vamsi Sangam //
// Theory of Programming //
/* ========== ========== ========== ========== */
#include <stdio.h>
#include <stdlib.h>
struct Edge {
int vertex;
struct Edge * next;
};
// Inserts Node to the Linked List by Head Insertion - O(1)
// Returns address of head which is the newly created node.
struct Edge * AddEdge(struct Edge * currentHead, int newVertex)
{
struct Edge * newHead
= (struct Edge *) malloc(sizeof(struct Edge));
newHead->vertex = newVertex;
newHead->next = currentHead;
return newHead;
}
void BreadthFirstSearch(
struct Edge * adjacencyList[],
int vertices,
int parent[],
int level[],
int startVertex
)
{
struct Edge * traverse;
int i, par, lev, flag = 1;
// 'lev' represents the level to be assigned
// 'par' represents the parent to be assigned
// 'flag' used to indicate if graph is exhausted
lev = 0;
level[startVertex] = lev;
// We start at startVertex
while (flag) {
flag = 0;
for (i = 1; i <= vertices; ++i) {
if (level[i] == lev) {
flag = 1;
traverse = adjacencyList[i];
par = i;
while (traverse != NULL) {
if (level[traverse->vertex] != -1) {
traverse = traverse->next;
continue;
}
level[traverse->vertex] = lev + 1;
parent[traverse->vertex] = par;
traverse = traverse->next;
}
}
}
++lev;
}
}
int main()
{
int vertices, edges, i, v1, v2;
printf("Enter the Number of Vertices -\n");
scanf("%d", &vertices);
printf("\nEnter the Number of Edges -\n");
scanf("%d", &edges);
struct Edge * adjacencyList[vertices + 1];
// Size is made (vertices + 1) to use the
// array as 1-indexed, for simplicity
int parent[vertices + 1];
// Each element holds the Node value of its parent
int level[vertices + 1];
// Each element holds the Level value of that node
// Must initialize your array
for (i = 0; i <= vertices; ++i) {
adjacencyList[i] = NULL;
parent[i] = 0;
level[i] = -1;
}
for (i = 1; i <= edges; ++i) {
scanf("%d%d", &v1, &v2);
// Adding edge v1 --> v2
adjacencyList[v1] = AddEdge(adjacencyList[v1], v2);
// Adding edge v2 --> v1
// Remove this if you want a Directed Graph
adjacencyList[v2] = AddEdge(adjacencyList[v2], v1);
}
// Printing Adjacency List
printf("\nAdjacency List -\n\n");
for (i = 1; i <= vertices; ++i) {
printf("adjacencyList[%d] -> ", i);
struct Edge * traverse = adjacencyList[i];
while (traverse != NULL) {
printf("%d -> ", traverse->vertex);
traverse = traverse->next;
}
printf("NULL\n");
}
printf("\nEnter a Start Vertex - ");
scanf("%d", &v1);
BreadthFirstSearch(adjacencyList, vertices, parent, level, v1);
// Printing Level and Parent Arrays
printf("\nLevel and Parent Arrays -\n");
for (i = 1; i <= vertices; ++i) {
printf("Level of Vertex %d is %d, Parent is %d\n",
i, level[i], parent[i]);
}
return 0;
}
Try using the above example given as practice as the sample input to your code, so that you can easily compare the results. Now, the important point here is when we insert a vertex into the Adjacency List, we follow Head Insertion to get O(1) Insertion. What happens due to this is that, the Linked List will have numbers in the descending order.
So, when we are applying BFS for adjacent vertices of a given node, the Vertex with the higher number is met first. And then we explore starting by that higher numbered Vertex. This is why whenever we had a choice in approaching a vertex, we preferred approaching from the vertex which had the bigger number, why…? Due to Head Insertion…! If you had used Tail Insertion, this would be reversed.
Other Implementations of BFS
This is the overview of Breadth First Search Algorithm. It has a computational complexity of O(|V| + |E|), which is pretty fast. But why O(|V| + |E|)…? If you think about the algorithm a little bit, we cover all the |V| vertices level-by-level, checking all the |E| edges twice (for an Undirected Graph). Once the level is set for a subset of vertices we don’t visit them again. Put an itty-bitty thought into it and I’m sure you’ll get the idea…! 😉 … But, the code above runs slower than O(|V| + |E|)… To achieve the proper complexity we must use a Queue.
We can use BFS in the following scenarios –
- Shortest Path or Quickest Path (if all edges have equal weight).
- Finding the Length of Shortest Path between two Vertices.
With the knowledge of BFS you can start solving Graph Theory related problems. It really depends on your logic how you will apply the BFS to the given problem. And there is only one way to develop it… Practice…! So, keep practicing… Feel free to comment your doubts..! Commenting is super easy if you are a Facebook, Twitter or a Google+ user…! So, don’t hesitate..! 😉 … Happy Coding…! 🙂