Bellman Ford Algorithm

Hello people…! In this post I will talk about another single source shortest path algorithm, the Bellman Ford Algorithm. Unlike Dijkstra’s Algorithm, which works only for a graph positive edge weights, the Bellman Ford Algorithm will give the shortest path from a given vertex for a graph with negative edge weights also. Due to this, the Bellman Ford Algorithm is more versatile, but, it’s speciality comes at a cost. The runtime complexity of Bellman Ford Algorithm is O(|V||E|), which is substantially more than that of Dijkstra’s Algorithm. Sometimes this algorithm is called Bellman Ford Moore Algorithm, as the same algorithm was published by another researcher.

Before we get started, there are a couple of things that we must understand. Firstly, why does Dijkstra’s Algorithm fail for negative edge weights and second, the concept of Negative Cycles.

Why does Dijkstra fail?

Consider, the graph below,

The Dijkstra’s Algorithm is based on the principle that, if S → V₁ → … → V_k is the shortest path from S → V_k then D(S, V_i) ≤ D(S, V_j). But in the above given graph, clearly that principle is violated. In the above graph, the shortest path from V₁ to V₃ is of length 3 units but the shortest path to V₄ is of length 1 unit which means that V₄ is actually closer to V₁ than V₃, which is contradicting Dijkstra’s principle.

Negative Cycles

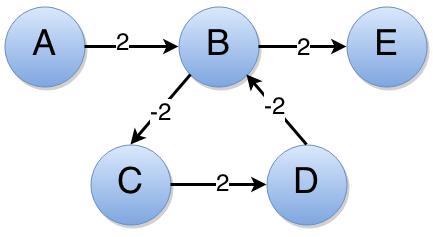
A Negative Cycle is a path V₁ → V ₂ → V₃ → … V_k → V₁ where the total sum of the edge weights in the path is negative. Consider the graph below –

The path B → C → D is a negative cycle as the path’s total weight would be -2. So, the distance from A → B is 2, but if we circle the cycle once, we would get the distance as 0, if we circle once more, we would get -2. Like this we could keep on circling as much as we want to reduce the shortest distance. Hence the shortest distance to the vertex B, E becomes indeterminate.

So, we want Bellman Ford Algorithm to solve these two issues. We want it to compute the shortest path even for a graph with negative edges and negative cycles. The Bellman Ford will accurately compute the shortest path for a graph with negative edges but the algorithm fails for a graph with negative cycles. But, the algorithm can tell you if a negative cycle exists or not. If it exists the solution it puts up is incorrect, otherwise, the solution given by Bellman Ford Algorithm is perfect. This sounds fine because logically there will be no shortest paths for a graph with negative cycles.

Unlike the Dijkstra’s Algorithm where we had to use a priority queue, we will require no additional data structure to code Bellman Ford Algorithm. This makes writing the code much easier. And the algorithm is pretty straight-forward too. Take a look at the pseudo-code of the Bellman Ford Algorithm given below –

bellmanFord(G, s)
	for all edges in G(V)
		D(V) = INT_MAX
		parent[V] = -1

	D(s) = 0

	for i = 1 to |G(V)| - 1
		for each edge (u, v) in G(E)
			if edge can be Relaxed
				D(v) = D(u) + weight of edge (u, v)
				parent[v] = u

	for each edge in G(E)
		if edge can be Relaxed
			return false

	return true

You may not understand the pseudo-code at the first look, here’s a step-by-step representation of it –

• Initialise the array which contains the shortest distances to infinity (a high integer value in the pseudo-code).
• Initialise the parent array which contains the parent vertices in the shortest path to NULL (or -1 if it is an integer array).
• Set the shortest distance of starting vertex to 0.
• Explore all the edges, and see if you can relax them. If you can, relax the edge and proceed with the exploration.
• Do the above operation |V| – 1 times.
• After that, do another exploration on the graph checking all the edges if they can be relaxed. If they can be relaxed, you can a negative cycle in the graph. Hence, return false.
• If the exploration gets finished successfully, the graph has no negative cycles and the data that you compute dis correct, so return true.

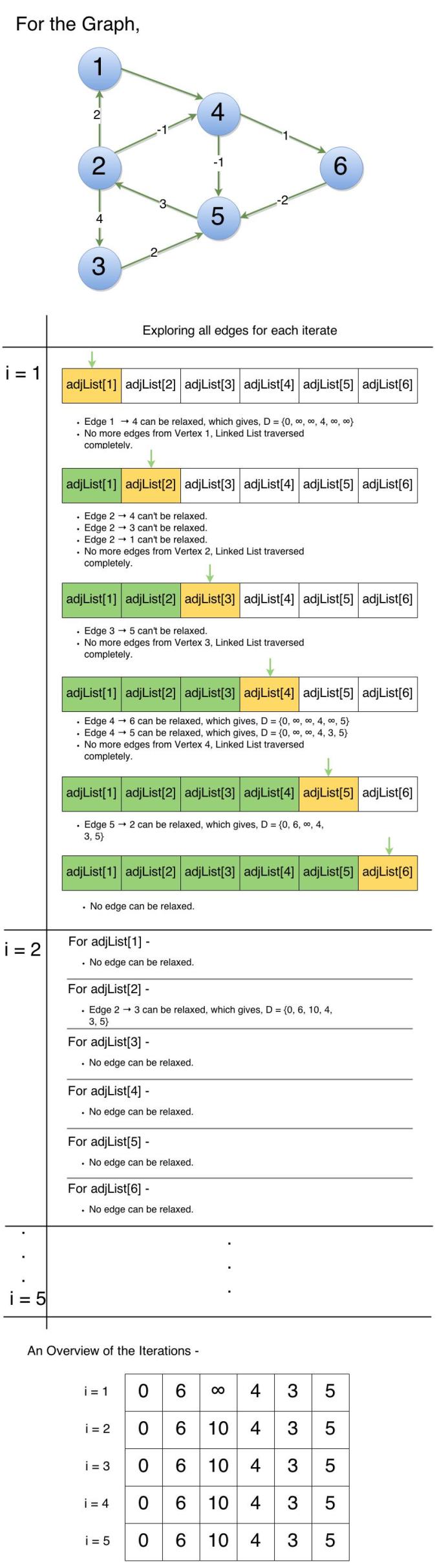
Now, what does exploring all the edges mean? If you are implementing the graph using an Adjacency List, it means to iterate over all the linked lists associated with all vertices. Now, what will be the sum of all the nodes in all Linked Lists in a given Adjacency List? Number of edges off course! So, we check all the edges from, edges of vertex 1 to vertex |V| in a linear manner. This whole operation takes O(|E|) time, which is repeated |V| – 1, so this part of the code takes O(|E||V|) time. Now, analyse the pseudo-code for a few minutes. Ask yourself how would you code this-ans-that. Now, when your mind is filled with the pseudo-code, look at the sketch below. The sketch below is sort of, “dry run” of the pseudo-code stated above –

The above sketch is self-explanatory. I hope you understand how the iterations go. In a way it looks like a very ordinary algorithm, without any greedy steps or partitions or so. The Bellman Ford Algorithm is pretty easy to code too. If you can work hard for an hour or two I’m sure you can code this algorithm. It does not require any priority queue or other tools. All you need to code Bellman Ford Algorithm is the pseudo-code. The pseudo-code is very important. Keep looking at the pseudo-code again-and-again whenever you get a doubt. I have put my code below for a reference, it is a C++ code –

/*
 * Bellman-Ford Algorithm
 *
 * Authored by,
 * Vamsi Sangam
 */

#include <cstdio>
#include <cstdlib>
#include <climits>

using namespace std;

// This is used to construct
// the Adjacency List
struct node {
	int vertex, weight;
	struct node * next;
};

// This is used to construct the Shortest Paths to all
// vertices, as we cannot return multiple values,
// we use a struct
struct pathInfo {
	int vertex, distance, parent;
};

// Adds a new edge into the Adjacency List
// Follows Head Insertion for O(1) Insertion
struct node * add(struct node * head, int vertex, int weight)
{
	struct node * p = (struct node *) malloc(sizeof(struct node));

	p->vertex = vertex;
	p->weight = weight;
	p->next = head;

	return p;
}

// Bellman-Ford Algorithm which takes the Graph (adjacencyList[]), starting vertex (startVertex),
// and an empty array shortestDistances[] as input. It applies the algorithm and keeps filling values
// into shortestDistances[]. It returns true if there are no negative edges, and vice-versa.
bool bellmanFord(struct node * adjacencyList[], int vertices, int startVertex, struct pathInfo shortestDistances[])
{
	struct node * traverse;
	int i, j, k;

	// Initialisation
	for (i = 0; i <= vertices; ++i) {
		shortestDistances[i].vertex = i;
		shortestDistances[i].distance = INT_MAX;
		shortestDistances[i].parent = -1;
	}

	// Setting distance to source = 0
	shortestDistances[startVertex].parent = 0;
	shortestDistances[startVertex].distance = 0;

	// The Algorithm that computes Shortest Distances
	for (i = 1; i <= vertices - 1; ++i) {		// Runs 'vertices - 1' times = O(|V|)
		for (j = 1; j <= vertices; ++j) {		// Runs as many times as the edges = O(|E|)
			// The code ahead basically explores the whole of Adjcency List,
			// covering one edge once, so the runtime of the code in this
			// block is O(|E|)

			traverse = adjacencyList[j];

			while (traverse != NULL) {
				if (shortestDistances[j].distance == INT_MAX) {
					// Important...!
					traverse = traverse->next;
					continue;
				}

				// Checking for Relaxation
				if (traverse->weight + shortestDistances[j].distance < shortestDistances[traverse->vertex].distance) {
					// Relaxation
					shortestDistances[traverse->vertex].distance = traverse->weight + shortestDistances[j].distance;
					shortestDistances[traverse->vertex].parent = j;
				}

				traverse = traverse->next;
			}
		}
	}

	// Checking for Negative Cycles
	for (j = 1; j <= vertices; ++j) {
		traverse = adjacencyList[j];

		while (traverse != NULL) {
			// Checking for further relaxation
			if (traverse->weight + shortestDistances[j].distance < shortestDistances[traverse->vertex].distance) {
				// Negative Cycle found as further realxation is possible
				return false;
			}

			traverse = traverse->next;
		}
	}

	return true;
}

int main()
{
	int vertices, edges, i, j, v1, v2, weight;

	printf("Enter the Number of Vertices -\n");
	scanf("%d", &vertices);

	printf("Enter the Number of Edges -\n");
	scanf("%d", &edges);

	struct node * adjacency_list[vertices + 1];
	//Size is made (vertices + 1) to use the
	//array as 1-indexed, for simplicity

	//Must initialize your array
	for (i = 0; i <= vertices; ++i) {
		adjacency_list[i] = NULL;
	}
	printf("Enter the edges -\n\n");

	for (i = 1; i <= edges; ++i) {
		scanf("%d%d%d", &v1, &v2, &weight);
		adjacency_list[v1] = add(adjacency_list[v1], v2, weight);
	}

 	//Printing Adjacency List
	printf("\nAdjacency List -\n\n");
	for (i = 1; i <= vertices; ++i) {
		printf("adjacency_list[%d] -> ", i);

		struct node * temp = adjacency_list[i];

		while (temp != NULL) {
			printf("(%d, %d) -> ", temp->vertex, temp->weight);
			temp = temp->next;
		}

		printf("NULL\n");
	}

	struct pathInfo shortestDistances[vertices + 1];
	int startVertex;

	printf("\nEnter a Start Vertex -\n");
	scanf("%d", &startVertex);

	if (bellmanFord(adjacency_list, vertices, startVertex, shortestDistances)) {
		printf("No Negative Cycles exist in the Graph -\n");
	} else {
		printf("Negative Cycles exists in the Graph -\n");
		// The Bellman-Ford Algorithm does not work with negative cycles,
		// all it can do is merely detect them, so when a negative cycle
		// is detected, the shortestDistances array has wrong values
		return 0;
	}

	printf("\n\nVertex    Shortest Distance to Vertex %d     Parent Vertex-\n", startVertex);
	for (i = 1; i <= vertices; ++i) {
		printf("%d         %d                                 %d\n", i, shortestDistances[i].distance, shortestDistances[i].parent);
	}

	return 0;
}

If you have any doubts regarding the algorithm feel free to drop a comment. I’ll surely reply to them. I hope my post helped you in learning the Bellman Ford Algorithm. If it did, let me know by commenting ! Commenting is super easy if you are a Facebook, Twitter or a Google+ user…! So, don’t hesitate..! 😉 Keep practicing… Happy Coding…! 🙂

You may also like –

• Dynamic Programming – Introduction and Fibonacci Numbers
• Binary Indexed Tree or Fenwick Tree
• Number Theory – Modular Arithmetic
• Graph Theory – Breadth First Search
• Quick Sort

More in the Navigation Page ! →